Recently, I was working on a computation problem that was based on dynamic programming. And of course, to store the sub-problem results, a cache was built to serve the purpose. Here is how the flow looked like after a cache was baked in:

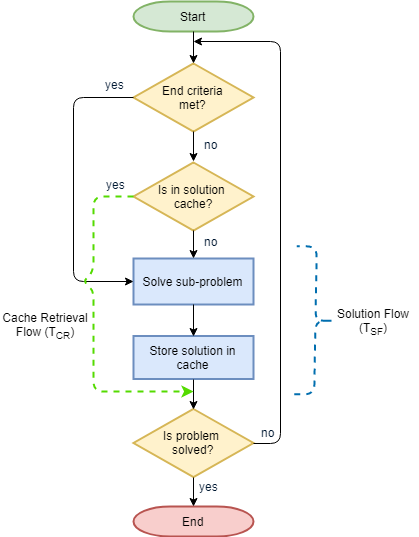
Typical solution, what seems to be the problem here?

After completing the solution and verifying that the function test cases are checked, I put on the hat of an SRE to identify the SLO for the solution based on the problem set. Enabled simple time profiling and what I observed was that the time to arrive at the solution was varying and wan't having a very strong correlation with the problem complexity. The moment the cache was removed, there was a strong correlation with the problem complexity. This anomaly kept me glued to my machine and I was deterred not to budge till the root cause was found.

What was causing the Anomaly with the cache baked in?

While solving a typical problem involving network or any IO operation, we take cache for granted as cache retrieval is faster than both. The problem that I was solving was a pure computation one without any IO activity. So, when the cache was baked in, the cache module was trying to save on the time spent on CPU cycles rather than any blocking IO calls. So, if retrieval of solution from cache takes longer than solving the problem itself, we are going to end up in trouble!!!

So, what are the factors that impact the time taken while introducing a cache? Here are some:

• The number of items in the cache - has a direct impact on the hash function to ensure collisions are avoided
• Time taken to add a solution into the cache - we have to ensure duplicate solutions aren't present
• Cache hit ratio - what if the solution isn't used later

What is an optimal model for caching?

Let's try deriving an equation that would help us make sure introducing the cache always results in saving the execution time. Here are some of the terms:

Tcr - Time taken to retrieve a solution from the cache for a given problem set

Tsf - Time taken to solve a sub-problem

Chit - Cache hit ratio (average case based on distribution of problem set)

N - The depth of the sub-problem solutions that is cached

Let's take the baseline case where adding cache doesn't minimally increase the time taken to arrive at a solution. So,

( (1 - Chit) * Tsf ) + ( Chit * N * Tcr )  <= Tsf

Chit * N * Tcr  <=  Tsf - [ (1 - Chit) * Tsf ]

Chit * N * Tcr  <=   Chit * Tsf

N  <=  Tsf / Tcr

For a given problem, Tsf, Tcr can be estimated to a good amount of precision while Chit is an approximate based on the probabilistic distribution of the problem set and the likely-hood of a sub-problem solution reuse. Based on the above, I restricted my cache module to store the solution for only sub-problems greater than a depth of 5. This resulted in a performance boost and the SLO was much more predictable for the execution time.

So, Never take a cache for granted and expect it to weave a magic in reducing the execution time of a module. Looking forward to hearing your thoughts!!